Modelling waning SARS-CoV-2 vaccination immunity
Summer Project | Data Science Intern
Hollingsworth group | Big Data Institute
During the summer of 2021 when I was there, the Hollingsworth group worked on cutting edge research and participated in multiple policy consortia which advised the government on the dynamics of the pandemic. One of the most pressing questions that summer was the future of COVID-19. The vaccination programme was starting to alleviate the pressure on the healthcare system. So the next question in line was whether waning vaccination immunity would lead to another insurgence of cases, as the susceptible group was replenished. This was my first and very rapid introduction to dynamic modelling. I was tasked with extending an existing difference-equation COVID-19 transmission-dynamic model to include vaccination and waning vaccination immunity. Moreover, I also tried to explore the suitability of a partially observed Markov process model to simulate the dynamics of transmission and/or estimate parameters of interest.
Research question
What could the impacts of waning SARS-CoV-2 infection and vaccination immunity be on the transmission dynamics in the UK in the short and medium term?
Background informationThe group had already published an age-structured deterministic model. The model was a discrete-time gamma delay-distributed SEIRS model (susceptible, exposed, infectious, recovered, susceptible) with symptomatic/asymptomatic and age-stratified transmission. Accounting for waning infection immunity, it attributed longer-lasting immunity to hospitalised patients than non-hospitalised. This model was to be extended to include vaccination and waning immunity from vaccination as well.
Crellen Thomas, Pi Li, Davis Emma L., Pollington Timothy M., Lucas Tim C. D., Ayabina Diepreye, Borlase Anna, Toor Jaspreet, Prem Kiesha, Medley Graham F., Klepac Petra and Déirdre Hollingsworth T. 2021. Dynamics of SARS-CoV-2 with waning immunity in the UK populationPhil. Trans. R. Soc. http://doi.org/10.1098/rstb.2020.0274.
Questions of interest
- Are vaccinated individuals less susceptible to infection than non-vaccinated ones?
- Does vaccinatoin protect against symptomatic disease? (Rather what is the proportion of asymptomatic cases in the infections reported by vaccinated individuals?)
- Do infected vaccinated individuals “replenish” their immunity upon recovery from infection?
- Is the effect the same for symptomatic and asymptomatic cases?
- Does vaccination protect against hospitalisation?
- Do the R boxes contribute to transmission?
Implications for policy
- Future of the pandemic i.e. what the winter of 2021 couold look like.
- Booster shot vs no booster shot ~ impact on transmission
- Waning immunity vs immune evasion vs increased contact i.e. how much vaccinated people transmit the Delta variant?
- Would vaccine passports be necessary or useful?
- What is the threshold for herd immunity with imperfect vaccination?
Some more background: the SIR model
To avoid diving straight into deep waters, let's consider a simple transmission dynamic model where three compartments exist: susceptible, infected, recovered. The compartments can be modelled in terms of absolute number of people in them or as a fraction of the total population. Accordingly, these are the equations that emerge.
| Compartment (absolute) | Equation | Compartment (relative) | Equation |
|---|---|---|---|
| \(S = S(t)\) the number of susceptible individuals; | \(\frac{dS}{dt} = -\beta \frac {S(t)} {N}\) | \(s(t) = \frac {S(t)} {N}\) the susceptible fraction of the population; | \(\frac{ds}{dt} = -\beta s(t) i(t)\) |
| \(I = I(t)\) the number of infected individuals; | \(\frac{dE}{dt} = \beta S I - (\mu + \sigma)E\) | \(i(t) = \frac {I(t)} {N}\) the infected fraction of the population; | \(\frac{di}{dt} = \beta s(t) i(t) - \gamma i(t)\) |
| \(R = R(t)\) the number of recovered individuals. | \(\frac{dI}{dt} = \sigma E - (\mu + \gamma)I\) $ = I - R$ | \(r(t) = \frac {R(t)} {N}\) the recovered fraction of the population. | \(\frac{dr}{dt} = \gamma i(t)\) |
POMP for S(E)IR
Now is a good time to mention POMP: partially observed Markov processes. As the name suggests, these are Markov processes which in addition to having a probability of occurring, also have a probability of being observed. This is great for modelling many biological phenomena, as the data collection process is imperfect, and survey coverage is rarely complete. For example, there is a probability that an individual will become infected and a probability that the infection will be recorded.
With this in mind, I tried to simulate the transmission dynamics using the SIR and SEIR (a model accounting for
the latent period of an infection, where an individual has been exposed to the disease but is not yet
infectious) models. To this end, I used the pomp package in R. The simulations relied on
the so-called “tau-leap” algorithm, one version of which is implemented in pomp via the euler
plug-in. This is a heuristic (hence more computationally efficient but less exact) version of the direct Gillespie
algorithm (more about the Gillespie algorithm in my
protometabolism modelling project here).
I was excited to get the SEIR simulations to work. I also tried to adapt the POMP model to account for gamma-distributed waiting times, but it did not quite work as expected. Therefore, I spent the remainder of my time with the group trying to understand why the results of the simulations did not correspond to the expectations. Reading source code and the documentation was challenging but rewarding, as I learned about the mechanics of the code very rapidly. I also wrote up and annotated all the working code for handover in my GitHub.
Extending the extant difference-equation model
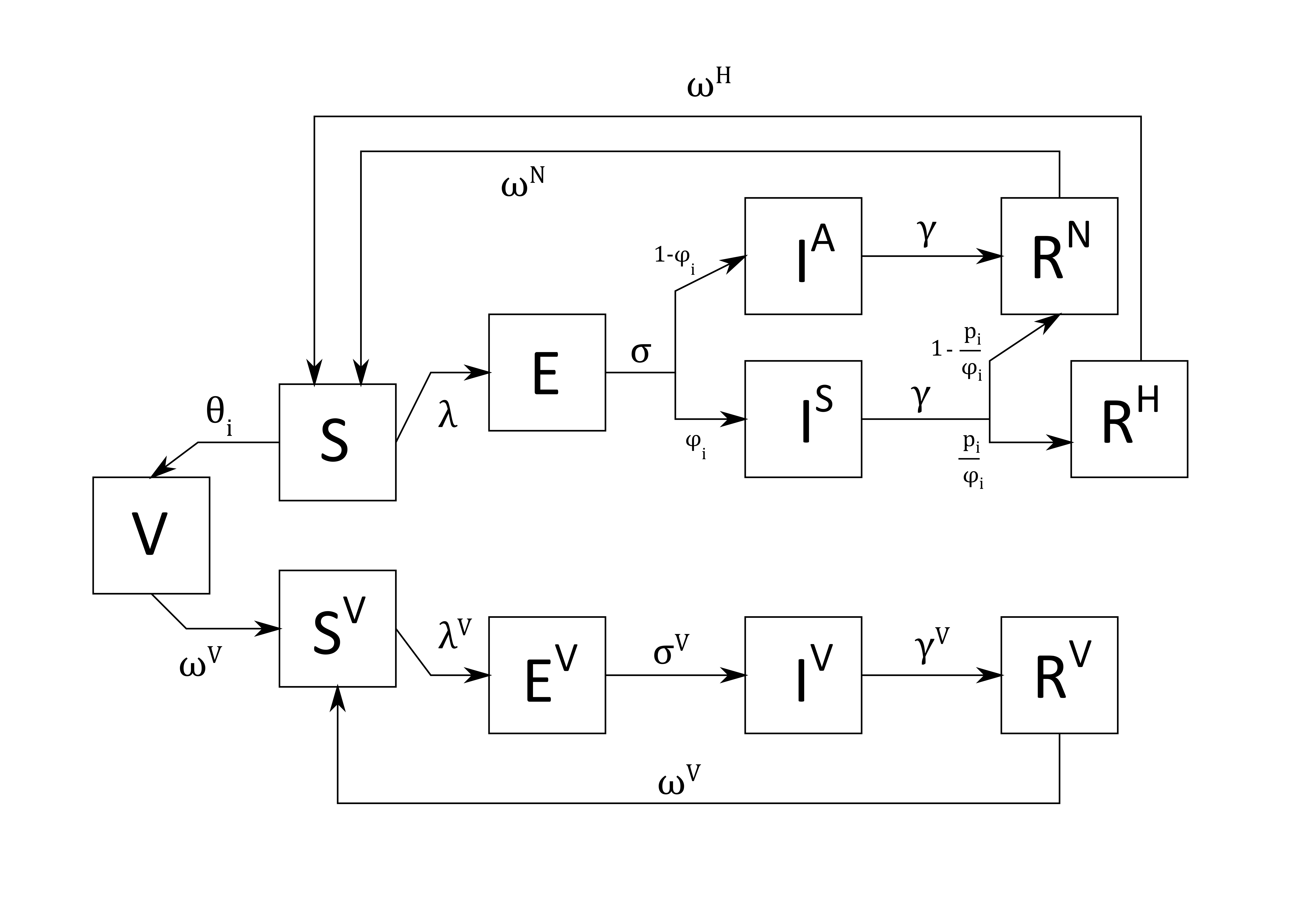
This may be a bold leap from S(E)IR, but below is the extended version of the published transmission-dynamic model.
Although I did not have time to adapt the original code to
It reflects completely different infection and recovery dynamics for vaccinated individuals.
There is waning immunity from infection recovery as
well as vaccination. The model assumes that individuals are vaccinated and gain immunity at some rate (probability)
constant per age group \(\theta_{i}\). This could be made continuously distributed
of needed: \(f_{t}(...)\).
The model also implies that \(E^{V}\), \(I^{V}\),
and \(R^{V}\) have their own \(F_{t}\) parameters
which differ between vaccinated and non-vaccinated individuals. Finally, vaccinated individuals who recover from
infection “replenish” their vaccination immunity, i.e., \(R^{V}\)
flows into \(V\).

Susceptible
\(S_{t+1} = S_{t} (1 - \theta_{i} - \lambda_{t+1}) + f_{t}(R^{N};o,\omega^{N}) + f_{t}(R^{H};o,\omega^{H})\)
\(S_{t+1}^{V} = S_{t}^{V} (1 - \lambda_{t+1}^{V}) + f_{t}(R^{V};s,\omega^{V}) + f_{t}(V;s,\omega^{V})\)
Vaccinated
\(V_{t+1} = V_{t} +S_{t}\theta_{i} - f_{t}(V;s,\omega^{V})\)
Exposed/infected
\(E_{t+1} = E_{t} + S_{t}\lambda_{t+1} - f_{t}(E;m,\sigma)\)
\(E_{t+1}^{V} = E_{t}^{V} + S_{t}\lambda_{t+1}^{V} - f_{t}(E^{V};q,\sigma^{V})\)
Infectious
\(I_{t+1}^{A} = I_{t}^{A} + (1-\phi_{i}) f_{t}(E;m,\sigma) - f_{t}(I^{A};n,\gamma)\)
\(I_{t+1}^{S} = I_{t}^{S} + \phi_{i} f_{t}(E;m,\sigma) - f_{t}(I^{S};n,\gamma)\)
\(I_{t+1}^{V} = I_{t}^{V} + f_{t}(E^{V};q,\sigma^{V}) - f_{t}(I^{V};r,\gamma^{V})\)
Recovered
\(R_{t+1}^{N} = R_{t}^{N} + f_{t}(I^{A};n,\gamma) + (1-\frac{p_{i}}{\phi_{i}}) f_{t}(I^{S};n,\gamma) - f_{t}(R^{N};o,\omega^{N})\)
\(R_{t+1}^{H} = R_{t}^{H} + \frac{p_{i}}{\phi_{i}} f_{t}(I^{S};n,\gamma) - f_{t}(R^{H};o,\omega^{H})\)
\(R_{t+1}^{VH} = R_{t}^{VH} + f_{t}(I^{V};r,\gamma^{V}) - f_{t}(R^{V};s,\omega^{V})\)
Parameters
The table below maps all symbols to their respective parameters.
| Symbol | Parameter | Symbol | Parameter |
|---|---|---|---|
| \(R_{0}\) | basic reproduction number | \(\omega^{VN}\) | immunity duration mean non-hospitalized vaccinated case |
| \(R_{c}\) | reproduction number under control measures for an entirely susceptible population | \(\omega^{VH}\) | immunity duration mean hospitalized vaccinated case |
| \(R_{t}\) | effective reporduction number in the presence of immunity | \(\omega^{VH}\) | immunity duration mean vaccinated individual |
| \(\theta_{i,t}\) | time-specificprobability of vaccination | \(s\) | immunity duration shape vaccinated |
| \(\sigma\) | latency period mean | \(\phi_{i}\) | probability of asymptomatic case given infection (non-vaccinated) |
| \(m\) | latency period shape non-vaccinated | \(\tau_{i}\) | probability of asymptomatic case given infection (vaccinated) |
| \(q\) | latency period shape vaccinated | \(p_{i}\) | probability of hospitalisaion given infection (non-vaccinated) |
| \(\gamma\) | infectious period mean | \(p_{i}^{V}\) | probability of hostpitalisation given infection (vaccinated) |
| \(n\) | infectious period shape non-vaccinated | \(C=c_{i,j}\) | contact matrix |
| \(r\) | infectious period shape vaccinated | \(\eta_{i}\) | relative susceptibility of age group $i$ |
| \(\omega^{N}\) | immunity duration mean non-hospitalized non-vaccinated case | \(\upsilon\) | relative infectiousness of asymptomatic cases |
| \(\omega^{H}\) | immunity duration mean hospitalized non-vaccinated case | \(\mu\) | relative infectiousness of vaccinated cases (symptomatic and asymptomatic??) |
| \(o\) | immunity duration shape non-vaccinated |
Next generation matrix
- Expected number of secondary infections in age group \(i\) resulting from contact with an index
case in age group \(j\): \(k_{ij} = \frac{\beta}{\gamma} \eta_{i} c_{i,j}
(\phi\nu+(1-\phi_{i}))\)
- \(\eta_{i}\) = relative susceptibility of of age group \(i\);
- \(\nu\) = relative infectiousness of asymptomatic cases.
- \(c_{i,j}\) = average number of daily contacts between a single individual in age group \(j\) and all individuals in age group \(i\);
- The basic reproduction number \(R_{0}\) is given by the spectral radius \(\rho(K)\) = the largest absolute eigenvalue of \(K\).
- As \(R_{0}\) is specified in the model, the transmission parameter \(\beta\) is left as a free parameter that is scaled to the correct value.
Force of infection
- \(\lambda_{i,t+1}\) = force of infection acting on a single
individual in age group \(i\) at time
\(t+1\): \(\lambda_{i,t+1} =
\beta \eta_{i} \sum_{j=1}^{M}
\frac {c_{i,j}N_{j}} {N_{i}} (\frac {I_{j,t}^{S} + I_{j,t}^{A}\nu}
{N_{j}})\)
\(\lambda_{i,t+1} = \frac {\beta \eta_{i}} {N_{i}} \sum_{j=1}^{M} c_{i,j}
({I_{j,t}^{S}+I_{j,t}^{A}\nu})\)
- \(M\) = number of discrete age groups (\(M = 15\));
- \(N_{i}\) = population size of age group i.
Although as a second-year student, at times I felt way out of my depth while working on this project, I learned so
much about advanced dynamic modelling techniques in such a short time. I adapted to the feeling of
not-quite-understanding what is happening and persevered, reading as much as I could around the topic, reading
code documentation and source code to understand where the errors were coming from. In this sense, it was a true
research experience, as after all, 99.9% of research is composed of getting an otherwise ingenious and elegant
idea to work.
I was fascinated by the considerations that a modeller has to make when simulating the behaviour of a complex system.
Parametrising highly complex dynamic models appeared to be a challenging and data-intensive task. Of course, tuning the
level of complexity was also guided by the end goal of the simulations. For a highly specific and pressing issue, such as
the future of the pandemic, expanding extant models was a necessary but demanding step.